|
|
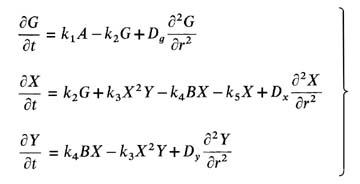
Particle Creation
1. 3D simulation showing a subatomic particle forming from an X potential ZPE fluctuation
This is a one dimensional cross section of a spherically symmetric particle extending radially
in three dimensions. Simulation parameters: Reaction volume radius = 50 spatial units, vacuum
boundary conditions, X potential seed fluctuation: 1 sigma in space, 3 sigma in time.
2. 3D simulation showing subatomic particle autogenesis (vertically expanded view)
This is a one dimensional cross section of a spherically symmetric particle extending radially
in three dimensions. Simulation parameters: Reaction volume radius = 50 spatial units, vacuum
boundary conditions, X potential seed fluctuation: 1 sigma in space, 3 sigma in time.
3. 3D simulation showing particle with higher core diffusion coefficient
Reaction volume: 3D, Radius = 50 spatial units, vacuum boundary conditions,
X potential seed fluctuation: 1 sigma in space, 3 sigma in time
Diffusion coefficient = 2 at center and decreases to 1 with sigma = 1.5 spatial units
4. 3D simulation showing particle with lower core diffusion coefficient
This is a one dimensional cross section of a spherically symmetric particle extending radially
in three dimensions. Simulation parameters: Reaction volume radius = 50 spatial units, vacuum
boundary conditions, X potential seed fluctuation: 1 sigma in space, 3 sigma in time.
Diffusion coefficient = 0.5 at center and increases to 1 with sigma = 1.5 spatial units.
5. 2D simulation showing a subatomic particle forming from an X potential ZPE fluctuation
This is a one dimensional cross section of circularly symmetric particle extending radially
in two dimensions. Simulation parameters: Reaction volume radius = 50 spatial units, vacuum
boundary conditions, X potential seed fluctuation: 1 sigma in space, 3 sigma in time.
6. 1D simulation showing a subatomic particle forming from an X potential ZPE fluctuation
This is a one dimensional plot of a particle formed in a one-dimensional reaction volume.
Simulation parameters: Reaction volume radius = 50 spatial units, vacuum boundary conditions,
X potential seed fluctuation: 1 sigma in space, 3 sigma in time.
7. 1D simulation showing a subatomic particle forming from a G and X potential ZPE fluctuation
This is a one dimensional plot of a particle formed in a one-dimensional reaction volume.
Simulation parameters: Reaction volume radius = 50 spatial units, vacuum boundary conditions,
X potential seed fluctuation: 1 sigma in space, 3 sigma in time.
8. 1D simulation showing two mutually bound particles forming a third
1D simulation of subquantum kinetics Model G showing a second particle nucleating into a bound
relation with the first and both particles then spawning a third one between them. This is a one
dimensional plot of a particle formed in a one-dimensional reaction volume. Simulation parameters:
Reaction volume radius = 50 spatial units, vacuum boundary conditions, X potential seed
fluctuation: 1 sigma in space, 3 sigma in time.
Particle Movement
1. 1D simulation showing particle moving down 2% G potential gradient
1D simulation of subquantum kinetics Model G showing a particle field pattern migrating down a
G potential gradient having a 2% slope. Demonstration of a new concept of field-induced
motion. This is a one dimensional plot of a particle formed in a one-dimensional reaction
volume. Simulation parameters: Reaction volume radius = 50 spatial units, periodic boundary conditions,
X potential seed fluctuation: 1 sigma in space, 3 sigma in time.
2. 1D simulation showing particle moving down 2% G potential gradient (zoomed view)
1D simulation of subquantum kinetics Model G showing a zoomed view of a particle field pattern
migrating down a G potential gradient having a 2% slope. Demonstration of a new concept of field-
induced motion. This is a one dimensional plot of a particle formed in a one-dimensional reaction volume.
Simulation parameters: Reaction volume radius = 50 spatial units, periodic boundary conditions,
X potential seed fluctuation: 1 sigma in space, 3 sigma in time.
3. 1D simulation showing particle moving down 1% G potential gradient
1D simulation of subquantum kinetics Model G showing a particle field pattern migrating down a
G potential gradient having a 1% slope. Demonstration of a new concept of field-induced
motion. This is a one dimensional plot of a particle formed in a one-dimensional reaction
volume. Simulation parameters: Reaction volume radius = 50 spatial units, periodic boundary conditions,
X potential seed fluctuation: 1 sigma in space, 3 sigma in time.
4. 1D simulation showing particle moving down 1% G potential gradient (zoomed view)
1D simulation of subquantum kinetics Model G showing a zoomed view of a particle field pattern
migrating down a G potential gradient having a 1% slope. Demonstration of a new concept of field-
induced motion. This is a one dimensional plot of a particle formed in a one-dimensional reaction volume.
Simulation parameters: Reaction volume radius = 50 spatial units, periodic boundary conditions,
X potential seed fluctuation: 1 sigma in space, 3 sigma in time.
5. Particle formed in G etheron velocity field
1D simulation of subquantum kinetics Model G showing a particle Turing wave field pattern moving in a
G etheron windthat moves from left to right. Simulation parameters: Reaction volume radius = 50
spatial units, vacuum boundary conditions.
Particle Trapped by X Potential Well or Hill
1. 1D simulation showing a subatomic particle trapped by an X well positioned at r = 1 unit
1D simulation of subquantum kinetics Model G showing a subatomic particle Turing wave field pattern
trapped by an X potential well positioned at r = 1 unit and turned on at t = 50. This indicates that for 1D
simulatons the Turing wave pattern of one particle can be trapped in the Turing pattern potential well of
a nearby partner particle that has the same polarity as the polarity it attempts to deploy at that location.
This trapping phenomenon may not necessarily be seen in more realistic 3D simulations. Simulation
parameters: Reaction volume radius = 50 spatial units, vacuum boundary conditions.
2. 1D simulation showing a subatomic particle trapped by an X hill positioned at r = 3 units
1D simulation of subquantum kinetics Model G showing a subatomic particle Turing wave field pattern
trapped by an X potential hill positioned at r = 3 units and turned on at t = 50. This indicates that for 1D
simulatons the Turing wave pattern of one particle can be trapped in the Turing pattern potential hill of
a nearby partner particle that has the same polarity as the polarity it attempts to deploy at that location.
This trapping phenomenon may not necessarily be seen in more realistic 3D simulations. Simulation
parameters: Reaction volume radius = 50 spatial units, vacuum boundary conditions.
3. 1D simulation showing a subatomic particle destroyed by an X hill positioned at r = 1 unit
1D simulation of subquantum kinetics Model G showing a subatomic particle Turing wave field pattern
destroyed by an X potential hill positioned at r = 1 unit and turned on at t = 50. This indicates that when
a subatomic particle field pattern encounters a small potential of polarity opposite to the field pattern it
attempts to deploy at that locoation, the particle wave can destabilize and collapse, rather than becoming
trapped. Simulation parameters: Reaction volume radius = 50 spatial units, vacuum boundary conditions.
4. 1D simulation showing a subatomic particle destroyed by an X well positioned at r = 5 units
1D simulation of subquantum kinetics Model G showing a subatomic particle Turing wave field pattern
destroyed by an X potential hill positioned at r = 1 unit and turned on at t = 50. This again indicates that
when a subatomic particle field pattern encounters a small potential of polarity opposite to the field pattern
it attempts to deploy at that locoation, the particle wave can destabilize and collapse, rather than becoming
trapped. Simulation parameters: Reaction volume radius = 50 spatial units, vacuum boundary conditions.