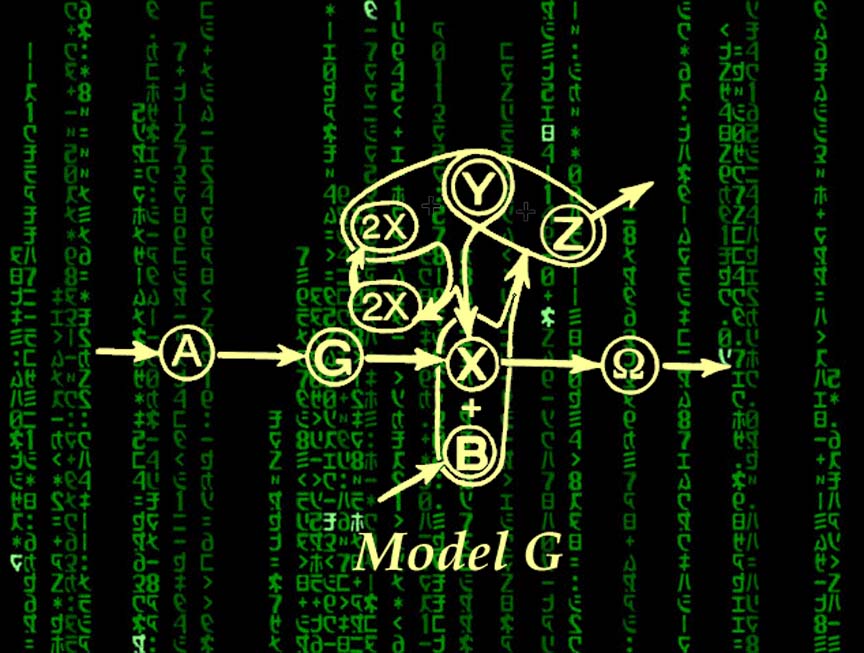
A collective mapping of the five ether reactions that form Model G

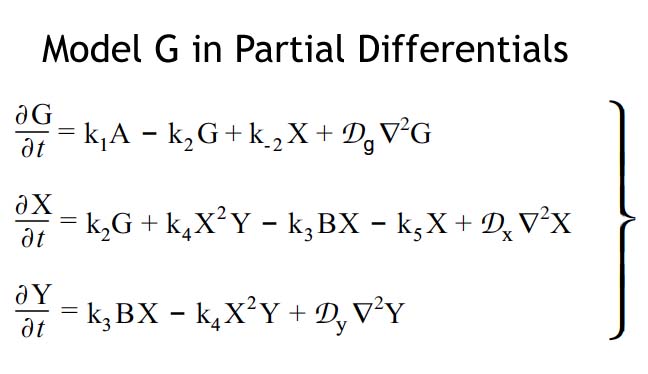Quantities A, B, G, X, and Y represent ether reaction concentrations. The k parameters represent the kinetic constants of the ether reactions. Finally, the Dx and Dy parameters denote the diffusion coefficients for the X and Y ethers.

Posted by:  Paul LaViolette

March 1, 2014
Model G Simulator

First a Brief Summary About Model G

Model G is a nonlinear ether reaction-diffusion system which subquantum kinetics postulates to be the generator of our physical universe.  It is simple and elegant.  It is the philosopher's stone that physicists have been seeking in their search for an effective unified field theory.  While very simple, this reaction-diffusion system exhibits highly complex behavior that so far has correctly predicted in advance a number of structural features of subatomic particles discovered in the last 15 years through particle scattering experiments.

Subquantum kinetics hypothesizes that spatial and temporal variations in the concentrations of the G, X, and Y ether variables displayed above constitute the matter and energy quanta that form the basis of our physical world.  These three ether variables and their source and sink ethers (A, B, D, and Ω) denote concentrations of  discrete etheric components called etherons that are hypothesized to fill all of space.  These entities are too small to ever be individually observed by physicists measuring instruments, but they are hypothesized to diffuse freely through space and to spontaneously react with one another.  Empty space and solid matter are both theorized to be filled with these ether on components.  The total medium composed of these intermixing and reacting components we call the transmuting ether.  Under the proper conditions (proper values for ether on concentration, kinetic constants, and diffusion coefficients), these collective reaction-diffusion processes are able to produce extended spatial structures called dissipative solitons which are accurate representations of subatomic particles.

The field potentials forming a material particle are in essence ether concentration patterns sustained by such reactions transpiring in and propagating through the ether.  The smallest observable objects, subatomic particles, then are actually not solid objects, but steady-state concentration patterns composed of far smaller underlying components.  Reacting and diffusing etherons form subatomic particles in much the same way that reacting and diffusing paraffin and oxygen molecules form the ordered plasma of a candle flame.  Both are examples of open systems  whose structural form is continuously generated and renewed by processes occurring at the subsystem  level in the system hierarchy.

.

The G ether concentration variations in Model G correspond to physically observable variations in gravity potential and the X and Y ether concentration variations correspond to physically observable variations in electric potential.  The reciprocal, complementary action of X and Y is what creates bipolarity, subatomic particles that exhibit the two electric polarities: positive vs. negative charge, or matter vs. antimatter configurations.   As a result of Model G's electrogravitic coupling, this same bipolarity characterizes the subatomic particle's gravity potential field yielding bipolar positive and negative mass states.  Magnetic effects are generated by moving electric fields; i.e., X-Y ether fluxes.

For more about subquantum kinetics, see the Starburst Foundation ether physics pages.

.

The Model G Simulator

Below is a simulator of this Model G ether reaction-diffusion system that simulates the three partial differential equations displayed above to show a particle structure spontaneously emerging from "empty" (matter-free) space.    Note that it runs best on newer computers; e.g. vintage 2010 and later with the most up to date web browser.  The simulator is currently set up to generate a one-dimensional representation of a dissipative soliton; i.e., representing the emergence of a primordial neutron from a spontaneously emerging zero-point energy fluctuation.  Just press the "run" button at the bottom.  The reaction-diffusion system parameters must be chosen to be close to the values given in the left column, otherwise the system will not generate a soliton structure.  You can experiment by altering the provided values and pressing "run" to see the outcome.  When finished you may reset the simulator by pressing the webpage reload button on your browser.  A similar simulator has been posted by Matt Pulver on the Blue Science website at: https://blue-science.org/sims/reaction_diffusion/.

The 10 parameters on the left are defined in Eqn. (8) in the paper by Pulver and LaViolette (2013).  They represent the following:  Parameters dx and dy set the values for the X and Y ether diffusion coefficients relative to the G diffusion coefficient; i.e. d_x = D_x/D_G and d_y = D_y/D_g.  Parameters a and b set the concentration values for the initial reactants A and B, and u and w set the concentration values for the final products Z and Ω.  Parameters g, p, q, and s set the ratios for various kinetic constants.  The homogeneous steady state concentrations for the reaction variables, G₀, X₀, and Y₀, are specified as follows: G₀ = (a + gw)/(q - gp),  X₀ = (pa + qw)/(q - gp), Y₀ = [(sX₀² + b)/X₀² + u]X₀ .  For ease of display, the simulator's graph plots the X reactant at one tenth of its actual concentration in order that its plotted wave amplitude be comparable to the wave amplitudes of the G and Y reactants.

The Starburst Foundation wishes to thank Matt Pulver for creating this Model G simulator.  Also thanks to David Jonsson for his contribution to the simulation effort and his suggestion that we develop a Model G simulator that could be run on a web browser.

.

Experiment No. 1: Showing the particle formation results of a fluctuation emerging in an ether environment that is either a) modestly supercritical, b) subcritical or c) excessively supercritical.

In playing with these values, you will find that a stable particle is formed when parameter g is within the range 0.092 to 0.1025.  Above the upper limit of this range, when g > 0.1025, the reaction system enters its subcritical mode and any ordered structures will progressively dissipate.  For example, choose g = 0.1026 to see what happens.  A subatomic particle will initially form due to the temporary core supercritical region created by the initial seed fluctuation.  But when the seed fluctuation recedes and the particle is left on its own, its amplitude will gradually diminish and it will ultimately vanish.  The simulation should be allowed to run several minutes to see this.  As one chooses progressively higher values of g, the reaction system will become increasingly subcritical and the nucleated particle will vanish in an increasingly shorter time.

So when g = 0.1025, the system is at its critical stability threshold.  At this value, Model G would be marginally stable, or could be said to be in a condition of having Lyapunov stability.  This would correspond in physics to the condition of perfect energy conservation, where a photon would neither blueshift nor redshift over time.  Based on the equation given above, for the chosen parameter values, this threshold would correspond to a steady state G ether concentration of G₀ = 15.59889.  We may identify this concentration with the zero gravitational potential; i.e., φ_G = 0.

When G drops below this threshold, i.e., for G < 15.599 or negative gravity potential values (φ_G <0), Model G will be supercritical.  But there is a range of G values in this negative G potential supercritical domain where Model G is able to adequately form a particle-like dissipative soliton.  This spans the g parameter range 0.092 < g < 0.1025. In terms of G concentration, this range would span  15.419 < G < 15.599, or in terms of gravity potential (φ_G = 15.599 - G), it would span the range  from -0.18 up to zero.

But when the g parameter drops below 0.092, the particle field pattern develops an oscillation in its inner shell that eventually causes progressive shell growth and the relentless nucleation of adjacent particles nested core-to-core.  This instability threshold corresponds to a G concentration value of G < 15.419, or gravity potential value of φ_G < -0.18.  You can observe this by choosing a g value of 0.091 or less.  As can be seen, the outer Y max shells of the soliton grow into particle cores.  At progressively lower values of g, or more negative values of φ_G, this periodic structure will extend and become more pervasive, eventually producing an extended space structure pattern resembling that generated by the supercritical Brusselator.  In a 3D simulation, this mode would produce a nested array of particle cores (e.g., closely packed neutron particle cores) and would actually be a realistic depiction of the inside of a neutron star.  In other words, this extended periodic structure would represent neutronium (neutron degenerate matter). The prevailing supercritical conditions would make the neutrons more stable and unlikely to decay into protons.

Note that a g parameter value of 0.091, would correspond to a φ_G potential of -0.197, so that the zero potential value in the simulation would itself be below the threshold of marginal stability by a 0.197.  Thus even the φ_G hills in the particle's soliton "Turing wave pattern" would be submerged into the supercritical regime.

.

Experiment No. 2: Showing how varying the diffusion coefficients of the X and Y reactants can alter the level of ether criticality and change the outcome of matter formation.

By either increasing the value of the Y diffusion coefficient (i.e., increasing parameter dy) or by decreasing the value of the X diffusion coefficient (i.e., decreasing parameter dx) the system becomes supercritical with wall to wall structure.  Try this.  Doing the opposite, causes the system to become subcritical and the soliton to dissolve.  For example, try decreasing dy or increasing dx.  This accords with the behavior of the Brusselator.  For example, eqn. 3-5 and 3-6 in Subquantum Kinetics, taken from Nicolis and Prigogine, 1977, refers to the Brusselator.  It shows that the ratio Dy/Dx in relation to the value of the concentration of initial reactant B is significant in determining the reaction system criticality; e.g., (D_y/D_x)^½ > [(B - 1)^½]/(B^½ - 1) to allow the formation of ordered patterns.  A similar equation able to apply to Model G would need to take into account the reverse reaction kinetic constants (which in the Brusselator are assumed to be zero).

.

Experiment 3: Showing how varying the concentration of the B ether reactant can change the criticality of space and thereby produce large scale structure in the universe through its effect on matter creation.

Also note that by increasing parameter b (increasing the concentration of ether reactant B), the reaction system becomes more supercritical and by decreasing parameter b (decreasing the B ether concentration) it becomes more subcritical.  Try this.  In previous publications, have suggested that a periodic spatial variation in B ether concentration  spanning hundreds of megaparsecs can create supercritical regions spaced apart by subcritical regions which may explain the development of galaxy cluster walls, strings, and voids that together form the cosmic web; see below.  That is, B would directly influence the rate of particle materialization in space.

.

Those interested in obtaining a version of this simulator that can be run on your computer, contact Matt Pulver.  His email address is given in the above mentioned IJGS paper.